Algorithm to Sum The Fibonacci Numbers
- Time:2020-09-07 12:13:31
- Class:Weblog
- Read:25
The Fibonacci numbers are defined as the following sequence, with the current item is the sum of the previous two items.
F(1) = 0
F(2) = 1
F(N) = F(N – 1) + F(N – 2) for N >= 3
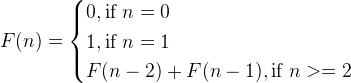
Fibonacci Equation
The first few Fibonacci numbers are: 0, 1, 1, 2, 3, 5, 8, 13, 21…
Of course, it is trivial to write a loop to sum the Fibonacci numbers of first N items.
1 2 3 4 5 6 7 8 9 10 11 12 | function sumOfFib(n) { let a = 0; let b = 1; let sum = 0; for (let i = 1; i < n; ++ i) { let c = a + b; a = b; b = c; sum += a; } return sum; } |
function sumOfFib(n) {
let a = 0;
let b = 1;
let sum = 0;
for (let i = 1; i < n; ++ i) {
let c = a + b;
a = b;
b = c;
sum += a;
}
return sum;
}Let’s define the S function the sum of first few Fibonacci numbers:
S(1) = F(1) = 0
S(2) = F(1) + F(2) = 1
S(3) = F(1) + F(2) + F(3) = 2
S(4) = F(1) + F(2) + F(3) + F(4) = 4
S(5) = F(1) + F(2) + F(3) + F(4) + F(5) = 7
…
We notice that
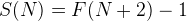
For example:
S(4) = F(6) – 1 = 5 – 1 = 4
S(3) = F(5) – 1 = 3 – 1 = 2
Using Induction to Prove the Fibonancci Sum Formula
S(1) = 0
S(2) = 1
Assume S(N) = F(N+2) – 1 stands.
S(N+1) = S(N) + F(N+1)
= F(N+2) + F(N+1) – 1
= F(N+3) – 1
And it also works for N+1!
Cancel Out the Fibonacci Numbers
We can rewrite the Fibonacci Formula as F(N) = F(N + 2) – F(N + 1).
Therefore, 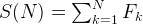
= F(2) – F(1) + F(3) – F(2) + F(4) – F(3) + …. F(N + 2) – F(N + 1)
Intermediate items are canceled out:
= F(N + 2) – F(1) = F(N + 2) – 1
How cool is that!
–EOF (The Ultimate Computing & Technology Blog) —
Recommend:5 Qualities of a Blog That Makes Money
How COVID-19 is Affecting Bloggers
How to Hire the Right Copywriter for Your Blog
5 Blogging Tips for Off-Road Enthusiasts
The Future of Work: How to Successfully Work Remotely
Javascript Function to Detect Capital String
Bruteforce/BackTracking Algorithm to Split Array into Fibonacci
How to Avoid Paying Too Much Fee when Cashing out Bitcoin via Wi
The Common Kodi Errors and Use of Free VPN for Linux
Java Pattern: Use Atomic Boolean to Return Single Usage Object
- Comment list
-
- Comment add