How to Construct Binary Search Tree from Preorder Traversal in P
- Time:2020-09-10 12:45:51
- Class:Weblog
- Read:38
Return the root node of a binary search tree that matches the given preorder traversal.
(Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val, and any descendant of node.right has a value > node.val. Also recall that a preorder traversal displays the value of the node first, then traverses node.left, then traverses node.right.)
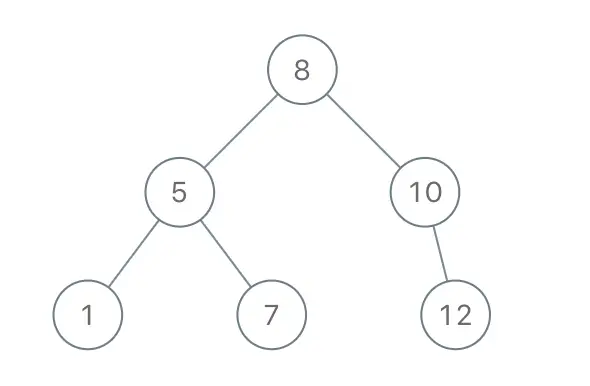
Input: [8,5,1,7,10,12]
Binary Search Tree
Output: [8,5,10,1,7,null,12]Note:
1 <= preorder.length <= 100
The values of preorder are distinct.
Divide and Conquer (Recursion) in Python
The root is the first element of the list. Then, we can find the sublist which has the elements smaller than the root, and the sublist with the elements larger than the root. Therefore, we can recursively construct the binary search tree using the divide-and-conquer technique.
The following Python recursion implementation is using the list list comprehension. You might also search the element and construct the list using the array slicing or simply passing the left and right index into the recursion.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | # Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def bstFromPreorder(self, preorder: List[int]) -> TreeNode: if len(preorder) == 0: return None root = TreeNode(preorder[0]) smaller = [x for x in preorder[1:] if x < preorder[0]] larger = [x for x in preorder[1:] if x > preorder[0]] root.left = self.bstFromPreorder(smaller) root.right = self.bstFromPreorder(larger) return root |
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def bstFromPreorder(self, preorder: List[int]) -> TreeNode:
if len(preorder) == 0:
return None
root = TreeNode(preorder[0])
smaller = [x for x in preorder[1:] if x < preorder[0]]
larger = [x for x in preorder[1:] if x > preorder[0]]
root.left = self.bstFromPreorder(smaller)
root.right = self.bstFromPreorder(larger)
return rootThe Java and C++ implementation of the same algorithm can be found here: How to Construct Binary Search Tree from Preorder Traversal? (C++ and Java)
Related Binary Tree Construction Algorithms
You may also like the following posts on the similar tree problems.
- Recursive Algorithm to Construct Binary Tree from Preorder and Postorder Traversal
- How to Construct Binary Search Tree from Preorder Traversal in Python?
- Algorithm to Construct Binary Tree from Preorder and Inorder Traversal
- How to Construct Binary Search Tree from Preorder Traversal? (C++ and Java)
- How to Construct String from Binary Tree?
- How to Balance a Binary Search Tree using Recursive Inorder Traversal Algorithm?
- How to Construct the Maximum Binary Tree using Divide-and-Conquer Recursion Algorithm?
- How to Construct Binary Tree from Inorder and Postorder Traversal using Depth First Search Algorithm (Recursion)?
- How to Construct Binary Tree from String (Binary Tree Deserialization Algorithm)
–EOF (The Ultimate Computing & Technology Blog) —
Recommend:3 Ways to Brainstorm New Blog Content
7 Good Blogger Tools For Working From Home
Can You Earn Bitcoin With Blogging?
Local Marketing Strategies: Five Tips for Lead Generation You Ca
How to Make Money from Blogging as a Small Business
6 Reasons Why Your WordPress Blog Is Getting Hacked
When to Revise Your Content Marketing Strategy
How To Develop Copywriting Skills To Engage Your Blog Readers
Five Tips to Lower Your Tax Bill in 2020
Bruteforce Algorithm to Compute the Maxmium Powerful Digit Sum u
- Comment list
-
- Comment add