How many different ways can £2 be made using any number of coins

Time：2020-09-10 12:45:51
Class：Weblog
Read：25

In the United Kingdom the currency is made up of pound (£) and pence (p). There are eight coins in general circulation:

1p, 2p, 5p, 10p, 20p, 50p, £1 (100p), and £2 (200p).

It is possible to make £2 in the following way:
1×£1 + 1×50p + 2×20p + 1×5p + 1×2p + 3×1p

How many different ways can £2 be made using any number of coins?

Depth First Search Algorithm

Let’s define a function f takes two parameters (amount and last). Thus, we can perform a Depth First Search (DFS) search based on the following

$tex_a70d0d338299cc17a407f6a31bf41c55 How many different ways can £2 be made using any number of coins? (Depth First Search and Dynamic Programming) algorithms DFS dynamic programming javascript math project euler$

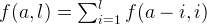
The f(0, x) is 1. We avoid duplicate solution by limiting the current coin strictly less or equal than the last coin.

function dfs(amount, last) {
    if (amount === 0) return 1;
    const coins = [1, 2, 5, 10, 20, 50, 100, 200];
    let ans = 0;
    for (let x of coins) { // iterate over the coins
        if (amount- x >= 0 && x <= last) { // non-bigger
            ans += dfs(amount - x, x);  // recursive dfs
        }
    }
    return ans;
}
 
console.log(dfs(200, 200));

function dfs(amount, last) {
    if (amount === 0) return 1;
    const coins = [1, 2, 5, 10, 20, 50, 100, 200];
    let ans = 0;
    for (let x of coins) { // iterate over the coins
        if (amount- x >= 0 && x <= last) { // non-bigger
            ans += dfs(amount - x, x);  // recursive dfs
        }
    }
    return ans;
}

console.log(dfs(200, 200));

The answer is 73682. We can also place a non-less coin and we need to call initially with last equal to 0:

function dfs(amount, last) {
    if (amount === 0) return 1;
    const coins = [1, 2, 5, 10, 20, 50, 100, 200];
    let ans = 0;
    for (let x of coins) { // iterate over the coins
        if (amount- x >= 0 && x >= last) { // non-smaller
            ans += dfs(amount - x, x); // recursive dfs
        }
    }
    return ans;
}
 
console.log(dfs(200, 0));

function dfs(amount, last) {
    if (amount === 0) return 1;
    const coins = [1, 2, 5, 10, 20, 50, 100, 200];
    let ans = 0;
    for (let x of coins) { // iterate over the coins
        if (amount- x >= 0 && x >= last) { // non-smaller
            ans += dfs(amount - x, x); // recursive dfs
        }
    }
    return ans;
}

console.log(dfs(200, 0));

Counting Number of Coins using Dynamic Programming Algorithm

We notice that we can save the intermediate results so that we don’t respawn too many recursions. The easiest way is to pass a dictionary (or hash map) as a last parameter.

The following Javascript code implements the Dynamic Programming Algorithm to count the coins based on the Recursive Depth First Search with Memoization Technique.

function dfs(amount, last, cached = {}) {
    if (amount === 0) return 1;
    const coins = [1, 2, 5, 10, 20, 50, 100, 200];
    // if it has been calculated, then return it
    if (typeof cached[amount + "-" + last] !== "undefined") {
        return cached[amount+ "-" + last];
    }
    let ans = 0;
    for (let x of coins) {
        if (amount - x >= 0 && x >= last) {
            ans += dfs(amount- x, x, cached);
        }
    }
    // save the result in the memo
    cached[amount+ "-" + last] = ans;
    return ans;
}
 
console.log(dfs(200, 0));

function dfs(amount, last, cached = {}) {
    if (amount === 0) return 1;
    const coins = [1, 2, 5, 10, 20, 50, 100, 200];
    // if it has been calculated, then return it
    if (typeof cached[amount + "-" + last] !== "undefined") {
        return cached[amount+ "-" + last];
    }
    let ans = 0;
    for (let x of coins) {
        if (amount - x >= 0 && x >= last) {
            ans += dfs(amount- x, x, cached);
        }
    }
    // save the result in the memo
    cached[amount+ "-" + last] = ans;
    return ans;
}

console.log(dfs(200, 0));

We can slightly rewrite this, using iterative approach. We sort the coins and start from the smallest coin. For each coin, we then incrementally update the answer.

function dp(amount) {
    let f = Array(amount + 1).fill(0);
    f[0] = 1;
    for (let x of [1, 2, 5, 10, 20, 50, 100, 200]) {
        for (let a = x; a <= amount; ++ a) {
            f[a] += f[a - x];
        }
    }
    return f[amount];
}

function dp(amount) {
    let f = Array(amount + 1).fill(0);
    f[0] = 1;
    for (let x of [1, 2, 5, 10, 20, 50, 100, 200]) {
        for (let a = x; a <= amount; ++ a) {
            f[a] += f[a - x];
        }
    }
    return f[amount];
}

The algorithmic complexity is O(NM) where N is the number of the coin-types and M is the amount. The space complexity is O(M).

–EOF (The Ultimate Computing & Technology Blog) —

Recommend：
How Small Companies Can Use Big Data
Hands Up and Step Slowly Away from the Keyboard: Why Good Execut
How to Improve Bad Blog Posts
5 Things That Bloggers Use in Their Craft
How To Increase Your Ecommerce Sales Using Social Media
Keyword Rank Tracking: What Newbie Bloggers Need to Know
Why Digital Products are the Key to Success for Bloggers
Why You Should Consider Alternative Domain Name Extensions for y
How to Create a Successful WordPress Site
How to Launch an E-Course the Right Way as a Blogger

Comment list

Comment add: Name：　Check：