Find the Queens That Can Attack the King

Time：2020-09-17 14:26:24
Class：Weblog
Read：29

On an 8×8 chessboard, there can be multiple Black Queens and one White King.

Given an array of integer coordinates queens that represents the positions of the Black Queens, and a pair of coordinates king that represent the position of the White King, return the coordinates of all the queens (in any order) that can attack the King.

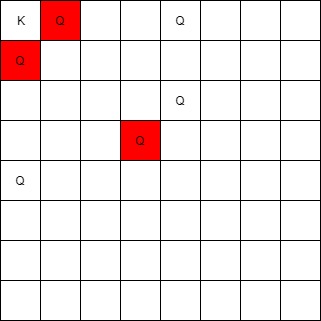
Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
Output: [[0,1],[1,0],[3,3]]
Explanation:
The queen at [0,1] can attack the king cause they’re in the same row.
The queen at [1,0] can attack the king cause they’re in the same column.
The queen at [3,3] can attack the king cause they’re in the same diagnal.
The queen at [0,4] can’t attack the king cause it’s blocked by the queen at [0,1].
The queen at [4,0] can’t attack the king cause it’s blocked by the queen at [1,0].
The queen at [2,4] can’t attack the king cause it’s not in the same row/column/diagnal as the king.

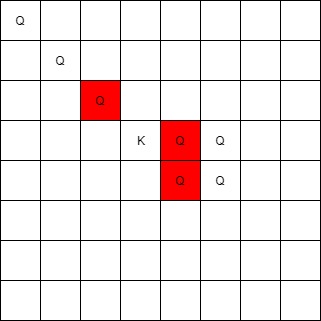
Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
Output: [[2,2],[3,4],[4,4]]

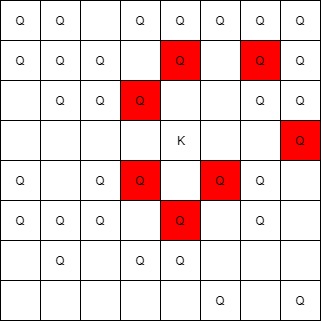
Input: queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
Output: [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]

Hints:
Check 8 directions around the King.
Find the nearest queen in each direction.

Find the Nearest Queen in Each Direction by Bruteforce Algorithm

We can start search in 8 directions from the position of the king, until we meet the nearest the Queen or the position has fall outside of the chess board.

In order to find if there is a queen in the current position, we can preprocess the list of given queens into a hash set.

class Solution {
public:
    vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {
        vector<vector<int>> r;
        int dir[][2] = {{0, 1}, {1, 0}, {1, 1}, {-1, 0}, {-1, -1}, {0, -1}, {-1, 1}, {1, -1}};
        unordered_set<string> qs;
        for (const auto &q: queens) {
            qs.insert(std::to_string(q[0]) + "," + std::to_string(q[1]));
        }
        for (int i = 0; i < 8; ++ i) {
            int dx = dir[i][0];
            int dy = dir[i][1];
            vector<int> pos(king);
            while ((pos[0] >= 0) && (pos[0] < 8) &&
                (pos[1] >= 0) && (pos[1] < 8)) {
                pos[0] += dx;
                pos[1] += dy;
                if (qs.count(
                          std::to_string(pos[0]) + "," +
                          std::to_string(pos[1]))) {
                    r.push_back(pos);
                    break;
                }
            }
        }
        return r;
    }
};

class Solution {
public:
    vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {
        vector<vector<int>> r;
        int dir[][2] = {{0, 1}, {1, 0}, {1, 1}, {-1, 0}, {-1, -1}, {0, -1}, {-1, 1}, {1, -1}};
        unordered_set<string> qs;
        for (const auto &q: queens) {
            qs.insert(std::to_string(q[0]) + "," + std::to_string(q[1]));
        }
        for (int i = 0; i < 8; ++ i) {
            int dx = dir[i][0];
            int dy = dir[i][1];
            vector<int> pos(king);
            while ((pos[0] >= 0) && (pos[0] < 8) &&
                (pos[1] >= 0) && (pos[1] < 8)) {
                pos[0] += dx;
                pos[1] += dy;
                if (qs.count(
                          std::to_string(pos[0]) + "," +
                          std::to_string(pos[1]))) {
                    r.push_back(pos);
                    break;
                }
            }
        }
        return r;
    }
};

Alternatively, we can use O(1) memory e.g. static board boolean flags.

class Solution {
public:
    vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {
        vector<vector<int>> r;
        int dir[][2] = {{0, 1}, {1, 0}, {1, 1}, {-1, 0}, {-1, -1}, {0, -1}, {-1, 1}, {1, -1}};
        bool board[64];
        std::fill(begin(board), end(board), false);
        for (const auto &q: queens) {
            board[q[0] * 8 + q[1]] = true;
        }
        for (int i = 0; i < 8; ++ i) {
            int dx = dir[i][0];
            int dy = dir[i][1];
            vector<int> pos(king);
            while ((pos[0] >= 0) && (pos[0] < 8) &&
                (pos[1] >= 0) && (pos[1] < 8)) {
                pos[0] += dx;
                pos[1] += dy;
                if ((pos[0] >= 0) && (pos[0] < 8) && 
                    (pos[1] >= 0) && (pos[1] < 8) && 
                    board[pos[0] * 8 + pos[1]]) {
                    r.push_back(pos);
                    break;
                }
            }
        }
        return r;
    }
};

class Solution {
public:
    vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {
        vector<vector<int>> r;
        int dir[][2] = {{0, 1}, {1, 0}, {1, 1}, {-1, 0}, {-1, -1}, {0, -1}, {-1, 1}, {1, -1}};
        bool board[64];
        std::fill(begin(board), end(board), false);
        for (const auto &q: queens) {
            board[q[0] * 8 + q[1]] = true;
        }
        for (int i = 0; i < 8; ++ i) {
            int dx = dir[i][0];
            int dy = dir[i][1];
            vector<int> pos(king);
            while ((pos[0] >= 0) && (pos[0] < 8) &&
                (pos[1] >= 0) && (pos[1] < 8)) {
                pos[0] += dx;
                pos[1] += dy;
                if ((pos[0] >= 0) && (pos[0] < 8) && 
                    (pos[1] >= 0) && (pos[1] < 8) && 
                    board[pos[0] * 8 + pos[1]]) {
                    r.push_back(pos);
                    break;
                }
            }
        }
        return r;
    }
};

As the board size is fixed 8×8, both the time and space complexity is O(1) constant.

–EOF (The Ultimate Computing & Technology Blog) —

Recommend：
Switching to a Blogging Career: Can You Afford to Work from Home
4 Features that Will Enhance Your Blog
Amazon Surpasses Google: Should you Change your SEO Strategies?
How to Optimize WordPress Categories and Tags
Blogging Royalties: Michelle Obama Interviewing Barack on her Po
Content Marketing: Expectations Vs Reality
Blogger Skills: LinkedIn and Microsoft’s Digital Skill Programs
5 Tips for Creating a Content Strategy for Your eCommerce Websit
5 Tips You Can Use to Launch a Successful Property Management Bl
Blogging and Gaming Finally Recognized as Professions

Comment list

Comment add: Name：　Check：