The Union Find (Disjoint Set) Implementation in Java/C++

  • Time：2020-09-07 12:03:44
  • Class：Weblog
  • Read：42
2091E060-120E-4C44-BAA3-7E4E0DF7BD55 The Union Find (Disjoint Set) Implementation in Java/C++ algorithms c / c++ implementation java

Java

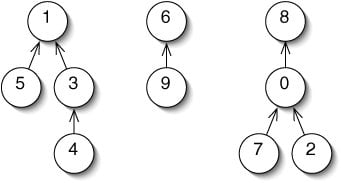
The Union-Find (Disjoint Set) is a commonly-used algorithm that can solve e.g. Minimal Spanning Tree. The following is a Java implementation of a Union-Find Class.

disjoint1 The Union Find (Disjoint Set) Implementation in Java/C++ algorithms c / c++ implementation java 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

package com.helloacm;
 
public class UnionFind {
    private int[] parent;
    public UnionFind(int n) {
        parent = new int[n];
        for (var i = 0; i < n; i++) {
            parent[i] = i;
        }
    }
 
    public int Find(int x) {
        if (x == parent[x]) {
            return x;
        }
        // compress the paths
        return parent[x] = Find(parent[x]);
    }
 
    public void Union(int x, int y)  {
        var px = Find(x);
        var py = Find(y);
        if (px != py) {
            parent[px] = py;
        }
    }
}
package com.helloacm;

public class UnionFind {
    private int[] parent;
    public UnionFind(int n) {
        parent = new int[n];
        for (var i = 0; i < n; i++) {
            parent[i] = i;
        }
    }

    public int Find(int x) {
        if (x == parent[x]) {
            return x;
        }
        // compress the paths
        return parent[x] = Find(parent[x]);
    }

    public void Union(int x, int y)  {
        var px = Find(x);
        var py = Find(y);
        if (px != py) {
            parent[px] = py;
        }
    }
}

The above algorithm uses O(N) space and requires O(N) time. Example usage:

1
2
3
4
5
6
7
8
9
10

package com.helloacm;
 
public class Main {
    public static void main(String[] args) {
        var uf = new UnionFind(5);
        System.out.println(uf.Find(3));
        uf.Union(3, 4);
        System.out.println(uf.Find(3)); // after join, 3's parent is 4.
    }
}
package com.helloacm;

public class Main {
    public static void main(String[] args) {
        var uf = new UnionFind(5);
        System.out.println(uf.Find(3));
        uf.Union(3, 4);
        System.out.println(uf.Find(3)); // after join, 3's parent is 4.
    }
}

This Java code prints 3 and 4.

C++ Disjoint Set / Union Find Algorithm Implementation

Similar, here is the C++ implementation of the Disjoint Set data structure. The union is a keyword in C++ and therefore we implement Union method instead:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class UF {
    public:
        UF(int N) {
            G.resize(N);
            std::iota(begin(G), end(G), 0);
        }
    
        int Find(int x) {
            if (x == G[x]) {
                return x;
            }
            return G[x] = Find(G[x]);
        }
    
        void Union(int x, int y) {
            int px = Find(x);
            int py = Find(y);
            if (px != py) {
                G[px] = py;    
            }            
        }    
    private:
        vector<int> G;
};
class UF {
    public:
        UF(int N) {
            G.resize(N);
            std::iota(begin(G), end(G), 0);
        }
    
        int Find(int x) {
            if (x == G[x]) {
                return x;
            }
            return G[x] = Find(G[x]);
        }
    
        void Union(int x, int y) {
            int px = Find(x);
            int py = Find(y);
            if (px != py) {
                G[px] = py;    
            }            
        }    
    private:
        vector<int> G;
};

Here, we use the iota from STL to easily assign incrementing values to the initial Group vector:

1
2

// G = {0, 1, 2, ...};
std::iota(begin(G), end(G), 0);
// G = {0, 1, 2, ...};
std::iota(begin(G), end(G), 0);

Compress Paths and Union Rules for Disjoint Set

As shown above - when in Find - we can compress the paths. Also, in the Union, we can either set G[px] = py or G[py] = px.

Choose a smaller group ID

This would be easiest - we compare the px and py value before setting the group:

1
2
3
4
5
6
7
8

void Union(int x, int y) {
  int px = Find(x);
  int py = Find(y);
  if (px != py) {
    if (px < py) swap(px, py); // make py smaller
    G[px] = py;    
  }            
} 
void Union(int x, int y) {
  int px = Find(x);
  int py = Find(y);
  if (px != py) {
    if (px < py) swap(px, py); // make py smaller
    G[px] = py;    
  }            
}

Merging into Smaller Size

Alternatively, we can allocate an addition array to store the sizes for each group and always merge the larger group into the smaller one:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class UF {
    public:
        UF(int N) {
            G.resize(N);
            std::iota(begin(G), end(G), 0);
            sizes.resize(N);
            std::fill(begin(sizes), end(sizes), 1);
        }
    
        int Find(int x) {
            if (x == G[x]) {
                return x;
            }
            return G[x] = Find(G[x]);
        }
    
        void Union(int x, int y) {
            int px = Find(x);
            int py = Find(y);
            if (px != py) {
                if (sizes[px] < sizes[py]) swap(px, py);
                G[px] = py;    
                sizes[py] += sizes[px];
            }            
        }    
    private:
        vector<int> G;
        vector<int> sizes;
};
class UF {
    public:
        UF(int N) {
            G.resize(N);
            std::iota(begin(G), end(G), 0);
            sizes.resize(N);
            std::fill(begin(sizes), end(sizes), 1);
        }
    
        int Find(int x) {
            if (x == G[x]) {
                return x;
            }
            return G[x] = Find(G[x]);
        }
    
        void Union(int x, int y) {
            int px = Find(x);
            int py = Find(y);
            if (px != py) {
                if (sizes[px] < sizes[py]) swap(px, py);
                G[px] = py;    
                sizes[py] += sizes[px];
            }            
        }    
    private:
        vector<int> G;
        vector<int> sizes;
};

--EOF (The Ultimate Computing & Technology Blog) --

Recommend：
Blogging and Finance Management: How to Secure Your Financial Fu
9 Easy-to-Use SEO Tips to Boost Your Site’s Visibility Today
How to Land Guest Blogging Opportunities in Under an Hour
Tips For Creating An Education Blog That Will Attract Followers
What Is Data Blending, And What Does It Have To Do With SEO?
7 Elements of a Perfect Social Media Video
9 Simple Strategies to Improve Sales Today
The Invisible Battle for Ad Space on Your Blog: Ad Fraud vs Ad S
How to Solve SMTP: Could Not Authenticate using Gmail + PHPMaile
The Reduce Function in Python
Share：Facebook Twitter
Comment list
Comment add